NEW DEMO
A Geometric Induction Example: the Tromino Puzzle
This demo of the Tromino Puzzle provides a geometric example of an induction argument
showing for any square grid having side length \(2^n\), with a single square occupied by a tile, that it is
always possible to fill in the remaining \(2^{2n}-1\) squares.
called trominoes or tiles, covering three squares each in an L form. To see the tiles click
![]() .
.
| If you want to use simple activities before you read about induction, click here: Activities |
Background: Mathematical induction, or induction for short, is a method for proving statements often involving positive integers, but is easily applied to situations in which one case depends on previous cases.
The principle of induction is a powerful method for confirming results arrived at by inductive reasoning. "Inductive reasoning involves collecting evidence from experiments or observations and using this information to formulate a general law or principle. Inductive reasoning attempts to go from the specific to the general , but even with large quantities of evidence the conclusion is not guaranteed. However, mathematics often uses an inductive process to formulate conjectures which are then subjected to rigorous deductive reasoning before they are accepted. Remember that a conjecture is a conclusion based on incomplete evidence - that is, a guess. Much can be gained from using experimental evidence to suggest conjectures and then applying deductive arguments to determine the truth or falsity of the conjecture. A number of important advances in science and engineering evolved in just this way." [1]
"The cycle of EXPERIMENTS - CONJECTURE - CHECK by DEDUCTIVE REASONING'S is very important in mathematics." [1]
The principle of induction that we state next is really a particular deductive checking procedure not reasoning by induction.
Principle of Mathematical Induction
1. You have a conjecture that you suspect is true for every positive integer. Prove that the conjecture is true for the case n = 1. |
Notes:
1. The assumption that your conjecture is true for n = k is called the induction hypothesis.2. Showing that the conjecture must be true for the next number k+1, is the rigorous check part of the principle.
3. Showing that the conjecture is true for n = 1 is the common starting point, but it is not the only way to start. You can start with any value of n and apply the two steps of the induction principle.Why does the induction principle work? You have proved the conjecture is true for n = 1 (or whatever the first value is that you use). By showing step 2 of the induction principle, that is whenever the conjecture is true for some integer it must also be true for the next integer, you have established that the conjecture is true for n = 2 (or the first value + 1). Now since it holds for n = 2, by the proof given for step 2, it must hold for the next integer as well, so it holds for n = 3 (or the first value + 2). Continuing in this way you have an argument that the conjecture is true for all integers. (This suggestive argument can be made rigorous in a variety of ways, such as by the use of the well-ordering principle.)
If you want further details and examples click More about induction for a pdf file that is a portion of [1].
The Tromino Puzzle: For a square grid \(2^n\) by \(2^n\) choose a single square. The rest of the grid can be tiled using trominoes.
For an example of a tiling click here
 .
The"white" square is the (random) single square that is chosen so the remainder of the grid can be tiled. (This image was contributed by Norton Starr. See the
Resources at the end of this demo.)
.
The"white" square is the (random) single square that is chosen so the remainder of the grid can be tiled. (This image was contributed by Norton Starr. See the
Resources at the end of this demo.)
Below we show two animations with different tilings on 4 by 4 grids; the random single square is colored yellow.

#1. |
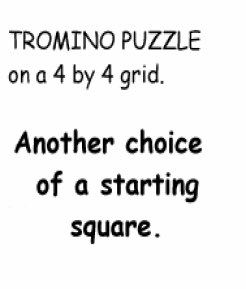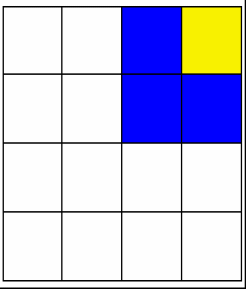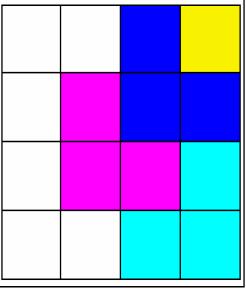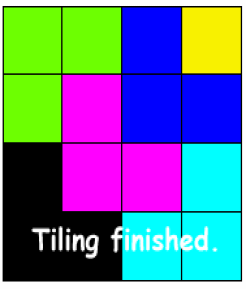
#2. |
Next we show how to apply the induction principle to prove the following conjecture:
For a square grid \(2^n\) by \(2^n\) choose a single square. The rest of the grid can be tiled using trominoes. Case: n = 1 For a square of side length 2 using Figure 1 it follows that any placement of the single white tile permits completion of the tiling by a tromino.

Figure 1. |
Before proceeding to step 2 of the induction argument, let's experiment a bit more.
Case: n = 2 Consider a square of side length 4 which is 4 copies of a square of side length 2 as shown in Figure 2.

Figure 2. |
Ideally we want to be able to prove that if we choose any of the 16 squares, the rest can be tiled by using trominoes. This would require 16 separate cases. Let's check a few of these to see if we are on the right track with our conjecture.
- Two cases were shown previously.
-
To check a few more cases click here
 .
Just imagine you had four different colors, 1 to 4 to obtain the tiles.
.
Just imagine you had four different colors, 1 to 4 to obtain the tiles.
- We can solve all the 16 cases (even though we didn't show them all). Thus we can say
For a square grid \(2^2\) by \(2^2\) choose a single square. The rest of the grid can be tiled using trominoes.
Explain why we know a 4 by 4 grid has 16 cases.
For a square with side length 4, the 16 cases can be done, but increasing the side length to be \(2^k\) increases the number of cases dramatically so that this strategy of "checking" all the cases is not feasible. Let's see how to reformulate the rigorous check procedure to avoid checking the16 cases individually.
Starting with the 4 by 4 square in Figure 2 choose a square to start with. It will be in one of the four 2 by 2 squares. For instance as in Figure 3. Next place a single tromino so that it occupies one square in each of the other three 2 by 2 squares; see Figure 4.
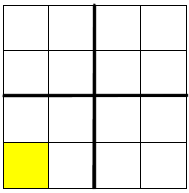
Figure 3. |

Figure 4.
|
IMPORTANT OBSERVATION:
|
Now each of the four 2 by 2 squares has one square "occupied", so by the proof of the case for n = 1, it can be tiled using (only) trominoes. It then follows that 4 by 4 square can be tiled using (only) trominoes, once a single square has been chosen. |
Thus we have proved the conjecture for the case n = 2 without considering all the cases individually. The observation above is the key to the proof of the general case, which we do next.
This more efficient approach suggests how to carry out the inductive process. We make the following induction hypothesis .
|
Given a positive integer k, assume that if a square grid \(2^k\) by \(2^k\) has one cell occupied by single square tile, then we can tile the rest of the grid using trominoes. |
Let's see how we use the induction hypothesis to prove the conjecture for a square grid \(2^{k+1}\) by \(2^{k+1}\). We start by noting that the square grid \(2^{k+1}\) by \(2^{k+1}\) is made up of four \(2^k\) by \(2^k\) square grids as shown in Figure 5. We randomly choose a single starting square in one of the quadrants of Figure 5. We then place a single tromino so that it occupies one square in each of the other three quadrants as shown in Figure 6. Now each of the four \(2^k\) by \(2^k\) quadrants contains a single starting square.
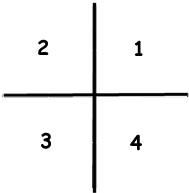 Figure 5. |
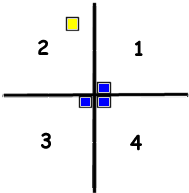 Figure 6. |
Finally apply the induction hypothesis to each of the four \(2^k\) by \(2^k\) quadrants to conclude that:
|
For a square grid \(2^{k+1}\)
by \(2^{k+1}\) choose a single square. The rest of the grid can be tiled using trominoes. |
The two steps of the principle of induction have been verified, so it follows that our conjecture is true for any \(2^n\) by \(2^n\) square.
Some Simple Activities
We have three SIMPLE activities which involve 4 by 4 grids for the game. The activities illustrate steps that you need to take when solving tromino games.
|
References and Auxiliary Resources:
- [1] B. Kolman and D. Hill, Student Solutions Manual for Elementary Linear Algebra, Ninth Edition, Prentice Hall, Upper Saddle River, New Jersey, 2008, page 21.
- This demo is a modification of a demo in the project Demos with Positive Impact , National Science Foundation's Course, Curriculum, and Labratory Improvement Program
under grant DUE 9952306. managed by David R. Hill and Lila Roberts. The project was based on submitted ideas from instructors. This demo was submitted by Norton Starr
at Amherst University; for his web site click here Professor Starr . Click
The Tromino Puzzle .
- For a list of Tromino Puzzle Print Resources and more Internet Sites compiled by Norton Starr click
here. (Warning; many of the sites may not be available.)
- For an 8 by 8 puzzle which you can "move" trominoes to attempt a solution click 8 by 8 puzzle.
- Here is another resource; click here for another 8 by 8 puzzle .
- At Wikipedia there is a very nice Geometrical dissection of an L-tromino; click here Wiki-tromino.
- There is another game called triminos; click here triminos . for more information