NEW DEMO

" This demo presents a class of matrices that can be used to illustrate basic topics covered in a beginning linear algebra course. This demo/student project can be used as a capstone exploration."

Prerequisites (Ideally): A beginning linear algebra course. The topics in the course should include vector spaces and eigen concepts. Students should be familiar with the concepts of matrices, inverses, reduced row echelon form, nonsingular, null space, eigenvalues, eigenvectors, and basis for a subspace.

Introduction: This is not intended to be a portion of a linear algebra book. Rather it could be used as a "refresher".

We provide a brief introduction to related items in simple terms about the linear algebra that we will use.

You can use the "Easy Jumps" below to see portions of the TOOLS needed here. For some one new to matrices and operations on them we recommend using the contents of the jumps as a crutch. We will use small matrices in our examples.

Easy Jumps
Matrices
Matrix Addition
Matrix Multiplication
Computing Matrix Multiplications
Properties of Matrix Products
Transpose of a Matrix
Identity Matrix
Nonsingular Matrix
Reduced Row-Echelon Form
Row-Echelon Form
Rank of a Matrix
Eigenvalues and Eigenvectors
Null Space
NOTES
Selected Resources

Matrices: Matrices are rectangular-shaped arrays that contain numbers arranged in rows and columns. Our matrices are often square. A square matrix has the same number of rows and columns. The contents of a matrix are called entries or elements and appear at the intersection of the rows and columns. For the following example we use small matrices. The dimensions of a matrix tells its size, the number of rows and columns, in that order. For example \( Q = \begin{bmatrix} 1 & -4& 2 \\ 1 & 0 & 2 \\ \end{bmatrix} \) is a 2 by 3 matrix and \( M = \begin{bmatrix} 1 & 2 \\ 3 & 5 \\ \end{bmatrix} \) is a 2 by 2 matrix.

A square matrix in general is denoted as an n by n matrix (or n x n), n a positive integer,

Matrix Addition: To add two matrices it is required that they have the same size. Let A and B be m x n matrices. Then the sum C = A + B is also an m x n matrix where the entries of C are the sums of the corresponding entries in A and B. Note that the following example illustrates how the entries of the C are computed using the entries of A and B. \[\text{Given matrices} \; A = \begin{bmatrix}3 & 4 & 7\\-1 & 1 & 0 \\ \end{bmatrix} \; \text{and} \; B = \begin{bmatrix}1 & 0 & -1\\2 & 1 & 1\\ \end{bmatrix} \;\text{, then the sum is}\; C = A + B =\begin{bmatrix} (3 + 1) & (4 + 0) & (7 - 1) \\ (-1 + 2) & (1 + 1) & (0 + 1) \\ \end{bmatrix} = \begin{bmatrix} 4 & 4 & 6 \\ 1 & 2 & 1 \\ \end{bmatrix} \text{.}\]

Matrix Multiplication: We can multiply matrices, but there are restrictions. Matrix multiplication is an operation in mathematics that produces a matrix from two matrices. To perform matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices A and B is denoted as AB or labeled a new name like C = AB.

An example using our matrices Q and M: the matrix product MQ (a 2 x 2 times a 2 x 3) is valid and the result is a 2 x 3 matrix, but the product QM is NOT valid. For an image of general matrix multiplication click this thumbnail .

Computing Matrix Multiplications: We use an operation called row-by-column product and sometimes called a dot product of a row and column. The dot product is an algebraic operation that takes two equal-length sequences of numbers and computes the sum of corresponding entries. This computation has the form \[ \begin{bmatrix}a_1 & a_2 & \cdots & a_n \end{bmatrix} . \begin{bmatrix}b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} = (a_1*b_1) + (a_2*b_2) + \cdots + (a_n*b_n) \] where both the row and column have n entries. (The single row is called a row vector and the single column is called a column vector. Note that the result of a dot product is a single number. Check the following example of a dot product. \[ \begin{bmatrix}-2 & 0 & 1 & 2\end{bmatrix} . \begin{bmatrix}1 \\ 1 \\ 3 \\ 2 \end{bmatrix} =11 \] Next we show the product of two matrices \(A = \begin{bmatrix}3 & 4 & 2\\-1 & 1 &\ 0\ \end{bmatrix}\) and \(B = \begin{bmatrix}1 & 0 & -1\\2 & 1 & 1\\ 1 & -1 & 3\\ \end{bmatrix}\) by using dot products of rows of A by columns of B.

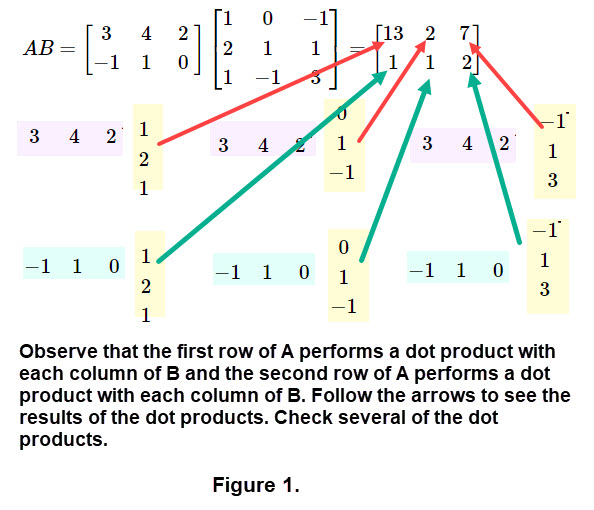
Let's test you about matrix multiplication. Here is a quick (optional) quiz; click this thumbnail and follow the directions . You can copy the matrices if you want to and figure the values of the dot products. (To check, look at a NOTES at the end of this demo; don't cheat.)

Properties of Matrix Products: Let A, B, and C be matrices, \(x\) vector, and r be a scalar (a number). Then \[A(B + C) = AB + AC \text{ and } A(rx) = rAx\] These properties are called distributive rules for matrix multiplication over matrix addition. The verification of these expressions uses the technique of matrix multiplication as discussed above. (This assumes that the sizes of the matrices and vector are valid for multiplication.)

Transpose of a Matrix: The transpose of a m x n matrix A is obtained by changing the rows of A into columns and columns of A into rows. The result, which is a n x m matrix is denoted by the symbol \(A^{T}\). For example for matrix \(A = \begin{bmatrix}3 & 4 & 7\\-1 & 1 & 0\\ \end{bmatrix}\) its transpose is \(A^{T} = \begin{bmatrix}3 & -1\\4 & 1\\7 & 0\\ \end{bmatrix}\).

Identity Matrix: An identity matrix is a square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by the notation \(I\) or \(I_n\) (where “n” represents the size of the matrix). In other words, an identity matrix is a matrix that, when multiplied by another matrix, leaves that original matrix unchanged, that is the identity of the original matrix stays. Here are some examples: \(I_2 = \begin{bmatrix}1 & 0\\ 0 & 1 \\ \end{bmatrix}\), \(I_3 = \begin{bmatrix}1& 0 & 0\\0 & 1 & 0 \\0 & 0 & 1\\ \end{bmatrix}\), \(I_5 = \begin{bmatrix}1& 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 \\0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{bmatrix}\). Here \(A = \begin{bmatrix}3 & 4 & 7\\-1 & 1 & 0\\ \end{bmatrix}\) is 2 x 3. Show that \(I_2 A = A\) and \(A I_3 = A\).

Nonsingular Matrix: A nonsingular matrix is a square matrix which is special. There are a variety of ways in which is special. Here is a simple example. If \(A\) is an n x n nonsingular matrix there exists another n x n matrix such that the product of these two matrices is \(I_n\). This other matrix is unique and its mathematical symbol is \(A^{-1}\), which is called the matrix inverse of \(A\). WARNING: The inverse matrix is "not" a reciprocal even though it acts like a reciprocal in matrix multiplication; \(AA^{-1} = I_n\) and \(A^{-1}A = I_n\).

If you have had a linear algebra course you should recognize the items that appear in the thumbnail below. For More information on how to recognize nonsingular matrices using linear algebra tools click this thumbnail . Some of the tools listed will appear later.

Reduced Row-Echelon Form: In linear algebra, Reduced Row-Echelon Form (RREF) is a specific form of a matrix that can be obtained through a sequence of elementary row operations. A matrix is said to be in RREF if it satisfies the following conditions:

1. All zero rows, if there are any, appear at the bottom of the matrix.
2. The first nonzero entry from the left of a nonzero row is a 1. This entry is called a leading one of its row.
3. For each nonzero row, the leading one appears to the right and below any leading one's in preceding rows.
4. If a column contains a leading one, then all other entries in that column are zero.

A matrix in RREF appears as a stair case pattern of leading ones descending from the upper left corner of the matrix.

The identity matrix \(I_n\) is in RREF. For example \(I_3 = \begin{bmatrix}1& 0 & 0\\0 & 1 & 0 \\0 & 0 & 1\\ \end{bmatrix}\). The matrices \(W = \begin{bmatrix}1& 0 & 0 & 0 & 8\\ 0 & 1 & 0 & 0 & -6\\0 & 0 & 0 & 1 & 4\\0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ \end{bmatrix}\) and \(Y = \begin{bmatrix}1& 6 & 0 & 3 & -2\\0 & 0 & 1 & 5 & 0\\0 & 0 & 0 & 0 & 0\\ \end{bmatrix}\) are in RREF. Any m x n matrix can be reduced to RREF. In order to reduce a matrix to RREF you use elementary row operations. In this demo we will not ask you to "REDUCE" a matrix to RREF. However, obtaining the RREF of a martix is a fundamental computation within linear algebra that has a impact for solving systems of linear equations, as it provides a clear and concise representation of the solutions. Click this thumbnail to see an example using row operations to solve a system of equations. (A portion of the material in this discussion of RREF came from Introductory Linear Algebra, An Applied First Course,8/e by Bernard Kolman and David R. Hill, Pearson, 2005.)
The RREF is similar to an REF. See the form of an REF blow.

Row-Echelon Form: Row Echelon Form (REF) of a matrix is a transformed version of the original matrix through a sequence of elementary row operations that satisfies the following conditions: A matrix is said to be in REF if it satisfies the following conditions:

1. Any row consisting entirely of zeros occurs at the bottom of the matrix.
2. For each row that does not contain entirely zeros, the first non-zero entry is 1 (called a leading 1).
3. For two successive (non-zero) rows, the leading 1 in the higher row is further left than the leading 1 in the lower row.

In other words, a matrix is in REF if it has the following structure:
Non-zero rows are above zero rows.
Each leading 1 is to the right of the leading 1 above it.
Every column contains at most one leading 1.
REF is similar to RREF but ,if a column contains a leading one, then entries in that column that are above the leading on need not be zero.
WARNING: the form of REF varies in definition. Some software may not require the leading ones. See the examples below. \[\text{RREF:} \; \begin{bmatrix}1& 0 & -2 & 0 \\0 & 1 & 4 & -1 \\0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \;\text{REF:} \; \begin{bmatrix}1& 3 & -2 & 0 \\0 & 1 & 4 & -1 \\0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \; \text{also REF:} \; \begin{bmatrix}2 & 3 & 4 & 5 \\0 & -2 & 1 & 2 \\0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \]

Rank of a Matrix: Computing the rank of a matrix involves reducing the matrix to its row echelon form (REF) or (RREF). The rank of a matrix is then equal to the number of non-zero rows in the reduced form.
Rank is a crucial tool for understanding the properties and behavior of matrices. The rank of a matrix has numerous real-life applications across various fields, including:

1. Linear Systems: In airports, the rank of a matrix is used to solve systems of linear equations, ensuring efficient flight scheduling and resource allocation.
2. Computer Graphics: In video game development, the rank of a matrix is employed to transform 3D objects and calculate camera positions, resulting in realistic graphics and gameplay.
3. Image Compression: The rank of a matrix is used to compress images by identifying the most important pixels and discarding redundant information.
4. Use your browser to find More applications.

Eigenvalues and Eigenvectors: To describe eigenvalues and eigenvectors we need to review several items from linear algebra.

Vectors: In mathematics, a quantity that has both magnitude and direction. Examples of such quantities are velocity and acceleration. Here is a sample image of a vector in a plane; click this thumbnail . For our purpose a vector will be a column matrix. In a two dimensions we have \(v = \begin{bmatrix} x \\ y\\ \end{bmatrix}\), in three dimensions we have \(w = \begin{bmatrix} x \\ y\\ z\\ \end{bmatrix}\) etc.

A Vector Space: A vector space V consists of a set of vectors and scalars (numbers) that is closed under (vector) addition and scalar multiplication. That is, when you multiply any two vectors in a vector space by scalars and add them, the resulting vector is still a member the vector space. In this demo our vector space will be either in two dimensions or three dimensions to keep things simple. For a vector space V that is a 2-dimensional Cartesian grid click this thumbnail for an image. For our examples we may use a portion of the standard Cartesian grid. Click this thumbnail for an image (we may change the size as needed). Here are other examples of vector spaces using matrices :

• The set of all 2 x 2 matrices.
• The set of all 10 x 10 matrices.
• The set of all columns with 4 entries.
• The set of all rows with 7 entries.
• The set of all 3 x 3 matrices of the form \( \begin{bmatrix}a & 0 & 0\\0 & b & 0 \\0 & 0 & c\\ \end{bmatrix}\), a, b, and c real numbers.

Linear Transformation: For this demo, a linear transformation is 'function' that assigns to each vector in our vector space V to a single vector also in the same vector space V. A linear transformation T is a function that satisfies two rules: (1) for vectors u and w in our vector space V, the result of T working on u + w is the same as the sum of T working on u + the result of T working on w. (2) for any (real) number k T multiplying the vector, k*u. is the same as k multiplying the result of T working on u. Usually these requirements are written as T(u + w) = T(u) + T(w) and T(k*u) = k*T(u).

Matrix_Multiplication_is_a_Linear_Transformation: Using the properties of matrix multiplication (listed earlier) verifies that matrix multiplication satisfies the rules to be a linear transformation.

Determinant: The determinant is a function of the entries of a square matrix and the result is a number. It is denoted as det(A), det A, or |A|, and its value characterizes some properties of the matrix and the linear transformation represented by the matrix. To compute the determinant for very small matrices is rather simple, but for larger matrices, numerical methods or specialized algorithms are often used. For small matrices (2 x 2, 3 x 3), the determinant can be computed using simple formulas: \[A = \begin{bmatrix}a & b\\ c & d \\ \end{bmatrix}, det(A)= ad - bc\] \[B = \begin{bmatrix} a & b & c \\d & e & f \\g & h & i\\ \end{bmatrix}, det(B) = a(ei - fh) - b(di - fg) + c(dh - eg) \] There is a pattern for these small matrices. To see it click this thumbnail

Computing the determinant det(A) in software uses techniques which first take the matrix A and determine a pair of matrices whose product is A. The two matrices involved are selected so that each of the two matrices can have their determinant easily computed. The product of those two determinants yields det(A). There are several different ways to generate the two matrices and in some software the techniques are not available to the public.

Eigenvalues and eigenvectors are fundamental concepts using square matrices in linear algebra, with far-reaching applications in various fields, including physics, engineering, computer science, and data analysis.

Eigenvalues: Scalars (numbers) that describe how a linear transformation affects a vector. An eigenvalue \(\mathbf{\lambda}\) represents the amount of stretching or shrinking a vector undergoes when transformed by an n x n matrix \(\mathbf{A}\).

Eigenvectors: Non-zero vectors that, when transformed by a matrix \(\mathbf{A}\), result in a scalar multiple of themselves, in other words, an eigenvector \(\mathbf{v}\) satisfies the equation \(\mathbf{Av = \lambda v}\), where \(\mathbf{\lambda}\) is the corresponding eigenvalue.

NOTE: in the equation \(\mathbf{Av = \lambda v}\) matrix \(\mathbf{A}\) is n x n and vector \(\mathbf{v}\) is n x 1, a column.

The matrix equation \(\mathbf{Av = \lambda v}\) can be rewritten using some matrix algebra into the form \(\mathbf{(\lambda * I_n - A) = O}\) where \(\mathbf{I_n}\) is the identity matrix and matrix \(\mathbf{O}\) is has all zero entries. Now compute \(\mathbf{det(\lambda * I_n - A) = det(O)} = zero\). The result can lead us to a polynomial in \(\lambda\) of degree n whose roots are the eigenvalues. Then we use the individual eigenvalues \(\mathbf{\lambda}\) in \(\mathbf{Av = \lambda v}\), to determine the corresponding eigenvector \(\mathbf{v}\).

Null Space: The null space of a matrix \(\mathbf{A}\), denoted as \(\mathbf{N(A)}\), is the set of all (column) vectors \(\mathbf{x}\) that satisfy the equation \(\mathbf{Ax = 0}\). In other words, it is the subspace of vectors that, when multiplied by \(\mathbf{A}\), result in the zero vector. (For this demo we will use square matrices.)

Subspace: A subspace is a vector space that is contained within another vector space. It inherits the operations of vector addition and scalar multiplication from the larger vector space. In our case if the matrix is n x n then the null space is a portion of the vector space of n x 1 columns.

Example: Let V be the vector space of all 4 x 1 vectors \(\mathbf{\begin{bmatrix}a \\ b\\ c \\d \\ \end{bmatrix}}\). Then the set of 4 x 1 vectors of the form \(\mathbf{\begin{bmatrix} 0\\ b\\ c \\0 \\ \end{bmatrix}}\), call it W, belongs in V and W is a subspace of V since (1) adding 2 vectors in W has the same form as those vectors in W and (2) any number times a member of W has the same form as those vectors in W. (Problem: name a simple vector that will be in any vector space V and in any subspace of V.)

Null Space Example 1: Lets start with a system of equations involving a 3 x 3 matrix \(\begin{matrix} 1x_1 + 2x_2 + 3x_3 = 0\\ 4x_1 + 5x_2 + 6x_3 = 0\\ 7x_1 +8x_2 + 9x_3 = 0 \\ \end{matrix}\). Next write this system in the form \(Ax = 0\); \(\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix}\) \(\begin{bmatrix} x_1 \\ x_2 \\ x_3\\ \end{bmatrix}\) \(\;=\;\begin{bmatrix} 0 \\ 0 \\ 0\\ \end{bmatrix}\). The first computational step is to compute the \( \text{rref}(A) = \begin{bmatrix} 1 & -2 & 0 \\ 0 & 0 & 1\\ 0 & 0 & 0 \\ \end{bmatrix}\). Next show the matrix equation \(\begin{bmatrix} 1 & -2 & 0 \\ 0 & 0 & 1\\ 0 & 0 & 0 \\ \end{bmatrix}\) \(\begin{bmatrix} x_1 \\ x_2 \\ x_3\\ \end{bmatrix} \;=\;\begin{bmatrix} 0 \\ 0 \\ 0\\ \end{bmatrix}\) and compute \(Ax\) to get the system of equations \( \begin{matrix} 1x_1 - 2x_2 + 0x_3 = 0\\ 0x_1 + 0x_2 + 1x_3 = 0 \\ 0x_1 + 0x_2 + 0x_3 = 0\\ \end{matrix} \). Now use algebra to get simple equations from each row; \(\begin{matrix} x_1 = 2x_2\\ x_3 = 0 \\ \end{matrix}\). Observe that we have no expression involving \(x_2\) so say \(x_2 = x_2\). Puttings together things we have the solution of matrix equation of \(Ax = 0\) is \(\begin{matrix} x_1 = 2x_2\\ x_2 = x_2 \\ x_3 = 0 \\ \end{matrix}\). The variable \(x_2\) can be any value and we get a solution. The null space for our matrix is all columns with 3 entries where the first entry is twice the second and the third entry is zero. Only when we have this pattern for a vector will \(Ax = 0\); for \(x_2 = r\) we have vectors of the form \(\text{r}\begin{bmatrix} 2\\ 1 \\ 0 \\ \end{bmatrix}\); for any value of \(r\) these vectors are the null space. Since each vector in the subspace involves the vector \(\begin{bmatrix} 2\\ 1 \\ 0 \\ \end{bmatrix}\) it is said to be a basis for the subspace.

Null Space Example 2: For a 4 x 4 matrix \(B\), find its null space and a basis for the null space. We skip the entries of \(B\) and find rref(B); \(\text{rref}(B) = \begin{bmatrix} 1 & 0 & -1 & -2 \\ 0 & 1 & 2 & 3\\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}\). Next determine a system of equations; \(\begin{bmatrix} 1 & 0 & -1 & -2 \\ 0 & 1 & 2 & 3\\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ \end{bmatrix}\) which leads to \(\begin{matrix} x_1 - x_3 - 2x_4 = 0 \\ x_2 + 2x_3 + 3x_4 = 0\\ \end{matrix}\). Solving for \(x_1\) and \(x_2\) we get \(\begin{matrix} x_1 = x_3 + 2x_4 \\ x_2 = - 2x_3 - 3x_4 \\ \end{matrix}\) and in addition \(x_3 = x_3\) and \(x_4 = x_4\). This indicates that \(x_3\) and \(x_4\) can be chosen to any numerical value. To find a basis for the null space lets set \(x_3 = r\) and \(x_4 = s\) we have 4 x 1 vectors \( \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ \end{bmatrix} = \begin{bmatrix} r + 2s \\ -2r - 3s \\ r \\ s \\ \end{bmatrix} = r \begin{bmatrix} 1 \\ -2 \\1 \\ 0 \\ \end{bmatrix} + s \begin{bmatrix} 2 \\ -3 \\0 \\1 \\ \end{bmatrix} \). The last 2 columns imply that every vector in the null space is a combination of \( \begin{bmatrix} 1 \\ -2 \\1 \\ 0 \\ \end{bmatrix} \text{and} \begin{bmatrix} 2 \\ -3 \\0 \\1 \\ \end{bmatrix} \) hence they are a basis for the null space

Applications of Null Space:

• Investment: In finance, a null space can represent the set of investment strategies that result in zero gain or loss, allowing investors to focus on More profitable opportunities.
• Power Distribution: In electrical engineering, a null space can represent the set of power distribution configurations that do not affect the overall system behavior, helping to optimize power distribution networks.
• Image Processing: In image processing, a null space can represent the set of image transformations that do not affect the overall image features, allowing for image compression and feature extraction.

====================================================

A description of this demo for students and instructors:

In some of the linear algebra TOOLS provided above there were examples. For example, if N is the set of all nonsingular matrices and S is the set of all n x n matrices for n equal to any positive integer, then N is a subset of S. Both types of sets are used for a variety of purposes which are designed to foster acquaintance, practice, and reinforcement of abstract and unifying ideas that are the cornerstone of linear algebra. By the end of the term students have encountered many sets of matrices and (hopefully) have acquired a reasonable set of skills that encompass the areas of matrix algebra, row operations, inverses, vector space notions, bases, and eigen concepts. Depending upon the type of course they may also have dealt with the geometric aspects of linear algebra which provide opportunities for visualization of a number of topics.

As instructors we want to have students draw together the topics of the course and see the interrelationships of the ideas that all too often seem to be compartmentalized as we progress through chapters of a text. One way to provide such an opportunity for student learning along these lines is to use a capstone set of exercises. These may be designed to encompass a number of topics, require that students experiment with a certain set of matrices, and quite possibly report findings by writing about properties they discover. In this regard the use of technology, namely software packages or even calculators, can be used to provide a format for experimentation. With such goals in mind an instructor needs a set of matrices that were not explored in depth previously in the course and which are fairly simple to generate and manipulate. This demo presents one such set that has been used successfully for several years with several different text books.

Definition: A reversal matrix is a matrix obtained by writing the rows and columns of an identity matrix \(\mathbf{I_n}\) in reverse order. (Recall, \(\mathbf{I_n}\) is square.)

EXAMPLES: The identity matrices are indicated by \(\mathbf{I_n}\) so we will use the notaton \(\mathbf{J_n}\) for the reversal matrices.
\[\mathbf{J_3} = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0\\ 1 & 0& 0 \\ \end{bmatrix}, \mathbf{J_4 } = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0\\ \end{bmatrix}, \mathbf{J_5 } = \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 \\ \end{bmatrix}\]

Lets consider using software to do the computations involving matrix equations which contain reversal matrices. There are a wide variety; some are commercial programs that require down loading and buying the program, in addition there are routines from the web that work quite well for the use in this demo. We will provide some brief descriptions bellow.

Large Software Packages

• GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB. The 4.0 and newer releases of Octave include a GUI. It is free.
• MATLAB is a widely used proprietary software for performing numerical computations. It comes with its own programming language, in which numerical algorithms can be implemented.
• Maple is a general-purpose commercial mathematics software package.
• Mathematica offers numerical evaluation, optimization and visualization of a very wide range of numerical functions. It also includes a programming language and computer algebra capabilities.
• For a large list of other software click Wiki List

Matrix Calculators available on the web

• These "calculators" provide easy access to compute matrix equations involved with reversal matrices. Each of these calculators have a different format for entering data. Some calculators don't have all the "tools" we discussed above. We will provide some hints on using some of the calculators but you should follow any directions included. Try several calculators to make a choice. There are quite a few.
  
  
• Click here Matrix Calculator; many of the "tools" are available. This on line linear algebra calculator has many features including multiplying, adding, and subtracting two square matrices of the same size. You can also move matrices to other tools. You need to experiment with features of this calculator to get comfortable with the capabilities. Click the thumbnail here to see the start of using features of this calculator. To show some features we have constructed an example. Use \(\mathbf{J_4}\) and \(\mathbf{I_4}\) and compute \(\mathbf{J_4 - I_4}\), then determine the eigenvalues and vectors of the computed matrix. Following are three thumbnails; view them in the order listed to see steps for the eigen values. View step #1: View step #2: View step #3: Try using this calculator with some easy tools. Click the CLEAN button to get a fresh start. (Our favorite.)
  
  
• Click here Symbolab; many of the "tools" are available. To see help in using this calculator click the thumbnail here . When you click Symbolab look at the list of 'TOPICS' at the left.
  
  
• Click here Linear Algebra Calculator; many of the "tools" are available but each tool must be used from a list independently so you need to reenter data for another tool. From the information from this calculator.
  How to use the Linear Algebra Calculator?
  Select a Calculator
  Browse through the extensive list of linear algebra tools and click on the one that fits your needs.
  Input
  Based on the calculator you've selected, fill in the required fields with the data you have.
  Calculation
  Click the "Calculate" button.
  Result
  Once you've inputted the necessary data and initiated the calculation, the calculator will process the information. After a brief moment, the computed solution will appear on the screen.
  (Ads appear in the various tools.)
  
  
• There are several desmos calculators. Use your browser to find them.

Sample of an assignment for students. (You can of course construct a number of other interesting investigations to suit your students and your course.)

For each of the following answer the result of the expression involving reversal matrices. Some answers require a matrix (M), others require a verbal description (V) of the type of matrix. Write the expression and answer on a sheet of paper. (Don't say it is a n by n matrix as an answer.)

1. \(\mathbf{J_4^T= \text{____________}(M)} \)
   
   
2. \(\mathbf{J_4^T = \text{is a____________ type of matrix.}(V)} \)
   
   
3. \(\mathbf{J_4^2 = \text{is ____________ }(M)} \)
   
   
4. \(\mathbf{J_4^{-1} = \text{is a____________ type of matrix}.(V)} \)
   
   
5. \(\mathbf{J_4^T*J_4 = \text{is ____________ }(M)} \)
   
   
6. \(\mathbf{J_4 = \text{is a____________ type of matrix. (V)} Hint: use\, answer\, to \,5} \)
   
   
7. \(\mathbf{J_4 + I_4 = \text{is ____________ }(M)} \)
   
   
8. \(\mathbf{\text{Let }W = J_4 + I_4.} \) \(\mathbf{\text{Find rref(W) = _______________(M)}}\)
   
   
9. Use the answer of #8 to find a basis for the null space of \(\mathbf{W = J_4 + I_4} \). The basis will be a set of vectors. Answer: \(\text{___________________}\)
10. Given that \(\mathbf{v} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \\ \end{bmatrix} \) is an eigenvector of \(\mathbf{J_4}\). Find the corresponding eigenvalue. \(\lambda = \text{_______} \). Hint, just recall \(\mathbf{J_4* v = \lambda * v }\).
11. In linear algebra, the trace of a square matrix A, denoted tr(A), is the sum of the elements on its main diagonal, \({\displaystyle a_{11}+a_{22}+\dots +a_{nn}}\).
    It is only defined for a square matrix (n × n).
    Use the table below to conjecture a formula for \(tr(\mathbf{J_n})\) , n a positive interger.
    

    n	3	4	5	6	7
    tr\((J_n)\)	1	0	1	0	1

    \(\text{Answer:________________________________________}\)
    
    
12. Use the table below to conjecture a formula for \(det(\mathbf{J_n})\) , n a positive interger.
    

    n	2	3	4	5	6	7	8	9
    det\((J_n)\)	-1	-1	1	1	-1	-1	1	1

    \(\text{Answer:________________________________________}\)
    
    
13. Use the table below to conjecture a formula for \(tr(\mathbf{W_n = J_n + I_n})\) , n a positive interger.
    

    n	3	4	5	6	7	8	9	10
    tr\((W_n\))	4	4	6	6	8	8	10	10

    \(\text{Answer:________________________________________}\)
    
    
14. The \(det(\mathbf{W_n = J_n + I_n})\) for n a positive interger is zero. Construct \(\mathbf{W_n}\) for n = 3, 4, 5, and 6. Then conjecture why \(det(\mathbf{W_n}) = 0)\) for all n.
    
    \(\text{Answer:________________________________________}\)

NOTES

Credits:
This demo is a modification of a demo in the project Demos with Positive Impact , National Science Foundation's Course, Curriculum, and Laboratory Improvement Program under grant DUE 9952306. managed by David R. Hill and Lila Roberts. The project was based on submitted ideas from instructors. This demo was suggested by Dr. David Zitarelli, Department of Mathematics, Temple University.

Assignments/Exercises:
To get a copy of the sample assignment as a PDF file click here Sample Assignment.
Look for the icon to print the file.

There is another set of questions that covers More topics. Click here More sample exercises.

Selected Resources

• wiki Exchange matrix(alias Reversal)
• handwiki Exchange Matrix
• wiki Trace