NEW DEMO

The two gifs that follow emphasize examples where segments and circles are used inside watches. Inherent are arrangements at various levels together with moving parts of a time piece. In addition, there are often 3 dials on a face of a chronograph watch. Typically the three dials register the time elapsed, a second dial (also referred to as a sub-second dial), a minute dial, and an hour dial. Click the thumbnail to see a chronograph picture. For more information go to Chronograph at wikipedia.

In this demo we illustrate the technique of the Monte Carlo simulation approach to estimate probabilities for two geometrically oriented problems involving line segments and another with circles within the unit circle. Prerequisites: Familiarity circles, radius, distance between points, and midpoint of a line segment; elementary probability ideas. There are algebraic requirements that influence how the experimental simulation steps are used for estimating probabilities.

We first state two problems in terms of the probability of making valid choices for pairs points in a circle of radius 1 centered at the origin (often called a unit circle).

Two Geometric Problems

Assumption: Let A and B be two points within the unit circle.

Problem 1. Estimate the probability that the length of a segment from A to B which is less than 1, will lie in the unit circle.

Problem 2. Estimate the probability that a circle centered at the midpoint of a segment from Problem 1 with radius 1/2 the length of the segment will lie entirely within the unit circle.

With students we should emphasize the algebraic and geometric concepts needed by anyone trying to solve either of the problems. This gives a real situation in which concepts play a roll for determination of a more complicated mathematical problem. Some of the tasks required to develop techniques to solve these problems are listed next. The two gifs below display the images for problems 1 and 2.

(a) How do we check that a pair of points lie in the unit circle?

(b) How do we compute the length of the segment between two points?

(c) How do we find the midpoint of a line segment?

(d) How do we determine if a circle with radius 1/2 the length of segment from A to B lies entirely within the unit circle?

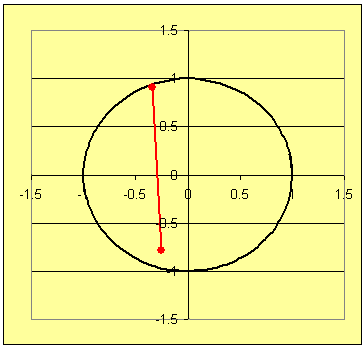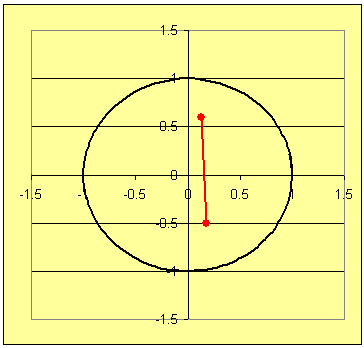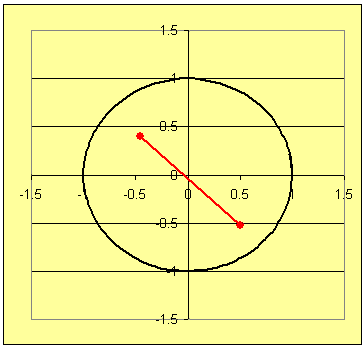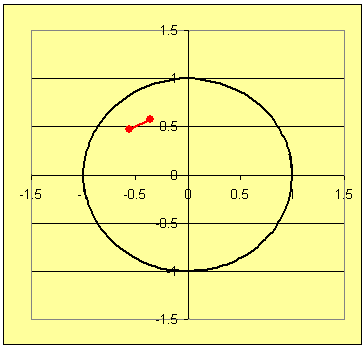
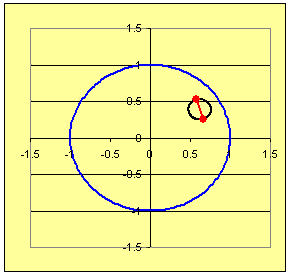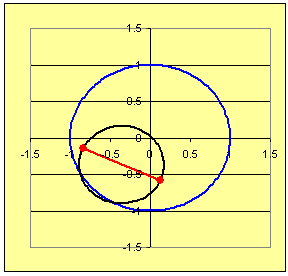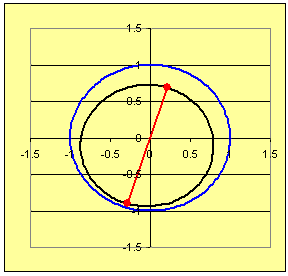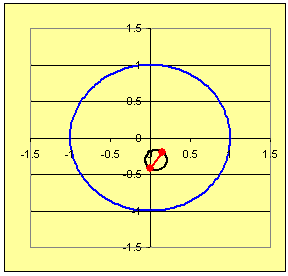
Techniques for answering (a) and (b) are used in Problem 1, while solutions for (a) - (d) are required for Problem 2.

Suggestions for working with students.

→ → → For (a): On the board or in a handout draw several unit circles with different choices for points A and B. (Specify the coordinates.) Choose some with both points inside the unit circle and others with 1 inside and the other outside, or both outside. Let the class experiment. Guide the class to get a well formulated criteria, then have them check things.

→ → → Tasks (b) and (c) are just are straight forward use of formulas that should be familiar.

→ → → For (d): Here is where some pictures will help, like those in Figures 1 and 2. Let students approximate the midpoint of the segments from A to B and then sketch a circle of radius 1/2 the distance from A to B centered at the midpoint. See Figures 3 and 4.

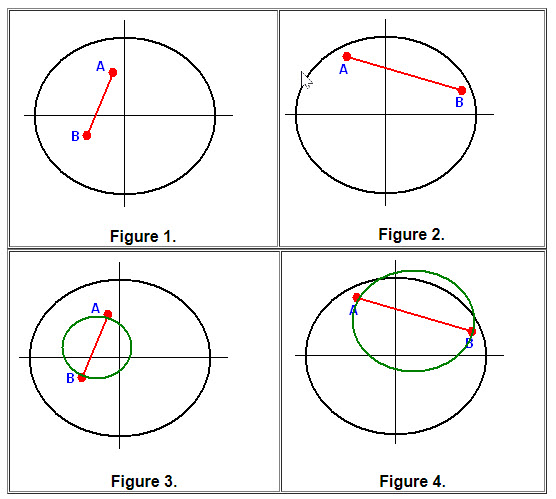
In diagrams like Figures 3 and 4 have students draw radii of the circles through points A and B. This may give them a feel for the idea discussed below. To see animations for drawing radii similar to situations depicted in Figures 3 click on thumbnail and for Figure 4 click on the thumbnail

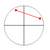
Now we need a way to determine from measurements if all the points along the circumference of the circle through points A and B are entirely within the unit circle. Recall that all such points must be a distance less than 1 from the origin. It is not practical to check the distance from the origin to each point on the circle from A to B, there are just too many. Our focus is on the distance from the origin so an alternative is to imagine that we have a rod extending the origin to the midpoint of the segment from A to B (see the black segment in Figure 5) and a radius of the circle through A and B that pivot around the end of the rod. As the radius pivots about the end of the rod the circle through A and B is traced. Since all the points on the circle through A and B are a distance of 1/2 times the length of segment through A and B from the midpoint we can observe the following:

If the distance from the origin to the midpoint of the segment from A to B (namely the length of the rod) + the radius of the circle through A and B is less than 1, then the entire circle through A and B is within the unit circle.

This is illustrated in Figure 5. Have students construct an algebraic test to determine if the circle through A and B lies within the unit circle.

The level of experience of students can be used by an instructor to gage how much the instructor has to contribute to obtain algebraic expressions to answer (a) - (d). Before any programs can be constructed to estimate the probability of a success for either Problem 1 or Problem 2 the foundations indicated above must be established. With the appropriate algebraic ideas developed from the geometry models, beginning students in a programming course who have had some practice in constructing programs with loops should be able to generate code to estimate the probabilities involved. If graphics to illustrate the geometry of the two problems is to included, then a discussion of how to easily draw a circle should be included.

Software Available:

As a reminder of our goal:

Two Geometric Problems

Assumption: Let A and B be two points within the unit circle.

Problem 1. Estimate the probability that the length of a segment from A to B which is less than 1, will lie in the unit circle.

Problem 2. Estimate the probability that a circle centered at the midpoint of a segment from Problem 1 with radius 1/2 the length of the segment will lie entirely within the unit circle.

In addition, here is a brief explanation of the Monte Carlo Method and how it works.

• The Monte Carlo Method is a computerized mathematical technique that allows people to quantitatively account for risk in forecasting and decision-making. At its core, the Monte Carlo Method is a way to use random samples of parameters to explore the behavior of a complex system. (In our case the parameters involve pairs of ordered pairs)
• Simulate processes that are time consuming.
• Run a large number of experiments in a short time-frame.
• Quickly adjust and repeat experiments.

We have developed software that illustrates the geometry involved with each problem and implements the Monte Carlo technique to estimate the probabilities of a success for each problem in both JAVASCRIPT and MATLAB. A part of the code is to use random number generators to obtain two ordered pairs within the unit circle and connect the pairs with a line, called a segment, and then determine if segment lies within the unit circle. The random number generators are different in the javascript from those in MATLAB, hence codes will vary. We will focus on the javascript code since our software here will not require you to have MATLAB.

Computing Estimates for PROBLEM 1.

To use the Monte Carlo method we need to keep track of the number of segments that are in the unit circle with length less than 1, and the number of segments that were in the unit circle but had length greater than 1. With this data we can compute the fraction to obtain an estimate of the probability for the segments which are in the unit circle with length less than 1. The number of segments of each type are computed in the code and shown to the user. However, there is another concern which results from using the random number generator. We explain this below.

The random number generator in javascript produces two ordered pairs with x and y coordinates in the interval [-1, 1], but one point or both may not be inside the unit circle. Basically we need to ignore such situations. In the Monte Carlo method you need to use a number of "input parameters". Look at Figure 6 and the items below it.

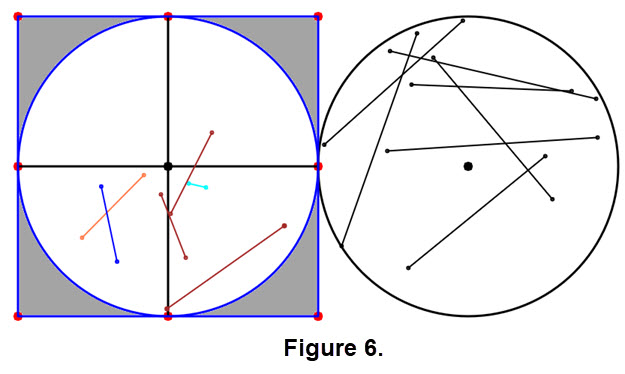
• Suppose that a user chose to enter 20 sets of two ordered pairs into our code, and the resulting figure generated appeared as Figure 6.
• Count the number of segments in the blue circle. Each segment is in the unit circle and has length less than 1. (There are 6.)
• Count the number of segments in the black circle. Each segment is in another unit circle, but the length is greater than 1. (There are 7.)
• You started with 20 pairs but the circles contain 13 segments. What happened? At least one of each of the other 7 "input parameters" had coordinates
  in the gray areas, hence they were ignored by the code.
• We drew a square around the blue circle to emphasize the gray areas. (When you use the code the square will not appear.)
• USER INFORMATION:
• → → → You will be asked to choose a number pairs of coordinates for input. (There are some restrictions.)
• → → → You will see output that verifies your input, and the counts in the blue circle and the black circle.
• → → → Follow the directions in the drop down boxes and the items near the bottom of the figure.
• → → → There is a "checker" for your percentage computation. It has more responses than just "CORRECT" or "INCORRECT".

In order to estimate the probability for the segments which are in the unit circle with length less than one you need to perform the Monte Carlo method a number of times, that is use our code. The results will lead to a sequence of estimates which may not "converge" to a particular percent right away. Each time you use our code the random number generator will probably result in varying values for an estimate even if you use the same number of input pairs. Write down your estimates until you feel you have a pattern.

To use our code for Problem 1 click here Estimate percent for Problem 1. You can click on a button to use the code again.

Computing Estimates for PROBLEM 2.

Problem 2 uses Problem 1 with the addition of requiring that we construct a circle centered at the midpoint of a segment that is in the unit circle so that the radius is 1/2 the length of the segment and that "new circle" will lie entirely within the unit circle. So the code to estimate the probability that this "new circle" will be in the unit circle requires "one more step". That step is an algebraic check and was discussed pin the paragraph above Figure 5 and illustrated in Figure 5. Thus two ordered pairs obtained via the random number generator from the interval [-1, 1] we have three "algebraic filters" that are used to get the circles within the unit circle as illustrated in Figure 7. Note the black segments and red circles; these were filtered out!

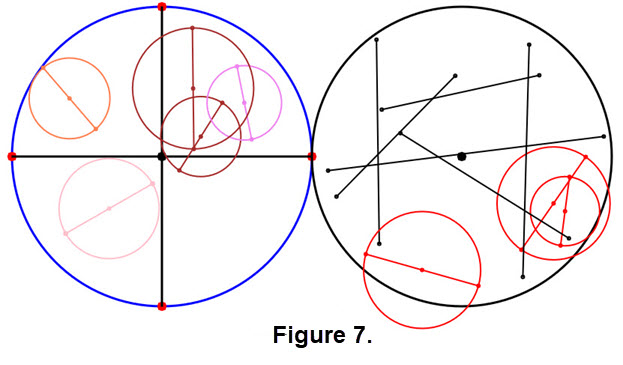
The user information for Problem 2 is similar to that for Problem 1. In the information below we have used bold for the changes.

• USER INFORMATION:
• → → → You will be asked to choose a number pairs of coordinates for input. (There are some restrictions.)
• → → → You will see output that verifies your input, counts the circles in the blue unit circle, and the segments and red circles in the black circle.
• → → → There is a "checker" for your percentage computation. It has more responses than just "CORRECT" or "INCORRECT".

To use our code for Problem 2 click here Estimate percent for Problem 2. You can click on a button to use the code again.

QUESTION: Why would you suspect that the percentage of circles in the unit circle is smaller than the percentage of the segments in the unit circle?

There is a variation of a problem in this demo. To modify Problem 2 "do not assume that the length of the segment from points A to B in the unit circle is less than 1." A minor modification of the code for Problem 2 will provide a way to estimate the percentage of the circles within the unit circle.

There is another demo that uses the MONTE CARLO method. Click here to view Simulation of a RAINBOW. Use this thumbnail for a picture.

Each of the problems discussed in this demo can be used to illustrate the use of some basic mathematical topics that play a fundamental role in the estimation of the solution of problems that require advanced mathematics to "solve" exactly. Determination of the exact probabilities for these problem use techniques from probability that are beyond the intended scope of this demo. For information on the theoretical probability of a success for the two problems see the Auxiliary Resources below.

• The basic ideas for the problems of the type discussed in this demo appeared as problems in mathematics journals.
• 1. Problem 178 (proposed by Roger L. Creech) in The Two-Year College Mathematics Journal, 1980, vol. 11 No. 5, p.336; a solution appeared in The Two-Year College Mathematics Journal, 1982, vol. 13 No. 2, p.151.
• 2. Problem 1092 (proposed by Roger L. Creech) in The Mathematics Magazine, 1980, vol. 53 No. 1, p.49; a solution appeared in Mathematics Magazine, 1981, vol. 54 No. 2, p.87.
• 3. A resource that discusses both of these problems and includes an analytic proof of probabilities of a success appears in an article by
  Joseph E. Chance and Pearl W. Brazier, "Two Problems That Illustrate the Techniques of Computer Simulation", Mathematics Teacher,
  1986, Vol. 79, No. 9, pp.726 - 731.
• 4. For a brief history of the Monte Carlo method go to History of Monte Carlo method.

SOFTWARE:

If you are interested in the javascript software, contact us. We also have similar code in MATLAB and a set of XCEL programs (old, but they still work) that are similar. For instance click here for a sample.