NEW DEMO
Trig Function Gallery
NOTE: the gallery page is best viewed in full screen mode.
Trigonometry has a long history. The Babylonians could measure angles, and are believed to have invented the division of the circle into 360ยบ. However, it was the Greeks who are seen as the original pioneers. The Greek mathematician, Euclid, was a prominent figure in geometry and trigonometry. Trigonometry developed from a need to compute angles and distances in such fields as astronomy, navigation, mapmaking, surveying, and artillery range finding. For more information click on Brief History of Trigonometry or for more in depth reading click on Further History.
Triangles and circles played important roles in the development of trigonometry. Certainly the relationships of angles and sides of triangles (specifically, right triangles) together with circles form visible means to understand basics in trigonometry. A unit circle is a circle with a radius of 1, centered at the origin (0, 0) in the Cartesian coordinate system, is used to define trigonometric functions (particularly sine, cosine, and tangent) in right triangle relationships. There are various diagrams involving unit circles that are used to aid in understanding trigonometric functions as shown in Figure 1.
Figure 1a appears as part of a source that includes an animation of the unit circle with angles changing from rotation involving right triangles; click this thumbnail
for quick look. For more diagrams click Unit Circle.
Figure 1b is from Unit Circle with sin, cos, and tan.
For another animation which moves right triangles around a circle and gathers data to graph the sine and cosine curves as the rotation moves click here
Sin and Cos Graphs via Rotating Triangles.
There are interactive animations that may provide further understanding of trigonometry;click any of the following Trig Index or Interactive Unit Circle.
There is a nice introductory discussion of basic ideas including circular functions, periodic functions, even & odd functions, and graphs of trigonometric functions at Basic Trigonometry. More sources of trigonometry including pictures, art, waves, etc. are listed in Other_Selected_Resources after the Gallery display.
Trig Gallery
The following is a gallery
of demos for illustrating selected families of functions. These figures and animations can be used by instructors in a classroom setting or by
students to aid in acquiring a visualization background relating to the change
of parameters in expressions for functions. Two file formats, gif and MP4, are used and should run on most systems. Originally, see the NOTES below the
gallery of animations, the animations were gif files which had no control for a user. The animations are now MP4 files which allow the user to easily control features
like stop and go, restart, and change the animation screen size. The controls are similar to those in You Tube. Click this thumbnail
to see an example. In this gallery a number of animations are rather small with information near the bottom; you can use the control to change the screen size for a better
view of the this area.
Gallery of Animations
| \(\large{\text{Generating Sine}}\) |
|
MP4 Animation |
| \(\large{\text{Sine Functions}}\) \(\mathbf{\large{ \text{f(x) = } \color{red}{a}\, \color{black}{sin (} \color{blue}{b} \color{black}{x ) +} \color{green}{d} }}\) \(\mathbf{\large{ \text{f(x) = } \color{red}{a}\, \color{black}{sin (} \color{blue}{b} \color{black}{(x + } \color{magenta}{c} \color{black}{)) +} \color{green}{d} }}\) |
|
Vary a
MP4 Animation Vary b MP4 Animation Vary c MP4 Animation Vary d MP4 Animation |
| \(\large{\text{Generating Cosine}}\) |
|
MP4 Animation |
| \(\large{\text{Cosine Functions}}\) \(\mathbf{\large{ \text{f(x) = } \color{red}{a} \,\color{black}{cos (} \color{blue}{b} \color{black}{x ) +} \color{green}{d} }}\) \(\mathbf{\large{ \text{f(x) = } \color{red}{a}\, \color{black}{cos (} \color{blue}{b} \color{black}{(x + } \color{magenta}{c} \color{black}{)) +} \color{green}{d} }}\) |
|
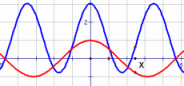
Vary a
MP4 Animation Vary b MP4 Animation Vary c MP4 Animation Vary d MP4 Animation |
| \(\large{\text{Generating Tangent}}\) |
|
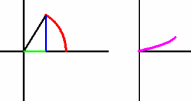
MP4 Animation |
| \(\large{\text{Tangent Functions}}\) \(\mathbf{\large{ \text{f(x) = } \color{red}{a}\, \color{black}{tan (} \color{blue}{b} \color{black}{x ) +} \color{green}{d} }}\) \(\mathbf{\large{ \text{f(x) = } \color{red}{a}\, \color{black}{tan (} \color{blue}{b} \color{black}{(x + } \color{magenta}{c} \color{black}{)) +} \color{green}{d} }}\) |
|
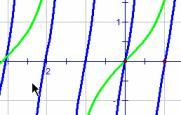
Vary a
MP4 Animation Vary b MP4 Animation Vary c MP4 Animation Vary d MP4 Animation |
| \(\large{\text{Generating Cosecant}}\) |
|
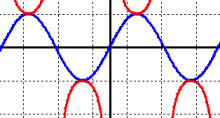
MP4 Animation |
| \(\large{\text{Generating Secant}}\) |
|
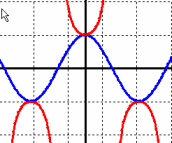
MP4 Animation |
| \(\large{\text{Generating Cotangent}}\) |
|
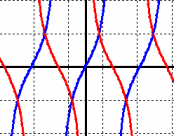
MP4 Animation |
| \(\large{\text{Inverse Sine}} \; \;arcsin\) \(\large{\text{Graph and Function}}\) |
|
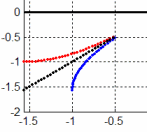
The graph:MP4 Animation The function: separate graphs MP4 Animation single graph MP4 Animation |
| \(\large{\text{Inverse Cosine}} \; \;arccos\) \(\large{\text{Graph and Function}}\) |
|
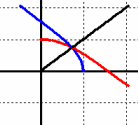
The graph:MP4 Animation The function: separate graphs MP4 Animation single graph MP4 Animation |
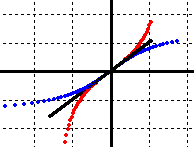
| \(\large{\text{Inverse Tangent}} \; \;arctan\) \(\large{\text{Graph and Function}}\) |
|
The graph: MP4 Animation The function: separate graphs MP4 Animation single graph MP4 Animation |
NOTES
- This demo is a modification of a demo in the project Demos with Positive Impact , National Science Foundation's Course, Curriculum, and Laboratory Improvement Program under grant DUE 9952306. managed by David R. Hill and Lila Roberts. The project was based on submitted ideas from instructors. The original demo appeared in 2006.
- Special thanks to Deane Arganbright of University of Tennessee at Martin and to Walter Hunter at Montgomery County Community College for their assistance with the development of the Excel files that were used to get this gallery. The book "Mathematical Modeling with Excel", by Erich Neuwrith and Deane Arganbright (Brooks-Cole) provides a rich source of information for developing Excel routines for mathematical instruction.
- This gallery was developed by David R. Hill, Temple University.
Other Selected Resources
- Brief History of Trigonometry
- Further History
- Unit Circle
- Unit Circle with sin, cos, and tan
- Trig Index
- Interactive Unit Circle
- Basic Trigonometry
- Various galleries
- Click to see basic trig function pictures
- Complex plots that show the magnitude as brightness
- Desmos showing a variety of trig curves
- Art with Trigonometric functions via geogbra
- Using trig for graphic art
- Wave Generation
- 742 Trig stock illustrations