NEW DEMO

MY FAVORITE MUG; Approximating Volumes of Solids of Revolution

The main objective of this demo is to show students how to Approximate the Volumes of Solids of Revolution. Students often have trouble estimating the volume of a container that has a non-standard shape. Much of the time their estimates for the volume of 'My Favorite Mug' are much too low. The developments of volumes of solids of revolution and Simpson's 1/3 Rule for approximation of integrals are combined to obtain a quite accurate measure of the volume of such mugs.

Lets consider that we have a student demonstation with hands on acess to a mug. To help this demo show the mug filling with beer. After the mugs are displayed to the class, lets focus on a particular mug (the student mugs may vary in size,) and give some information about it; the particular mug is 12oz a nd other data. Provide leading questions about My Favorite Mug to incorporate a discussion. Then give students more data and directions as shown next.

Performing the Estimation:

• Using a measuring tape determine the circumference of (your) 'My Favorite Mug' at the top, middle, and bottom.
• Compute the radii of the corresponding cross sections.
• Follow with an introduction to Simpson's 1/3 Rule

An instructor can choose how much of the topics that follow to use: Estimating Area Under a Curve and Estimating Volume of Solids, each with Simpson's 1/3 Rule.

Estimating Area Under a Curve using Simpson's 1/3 Rule:

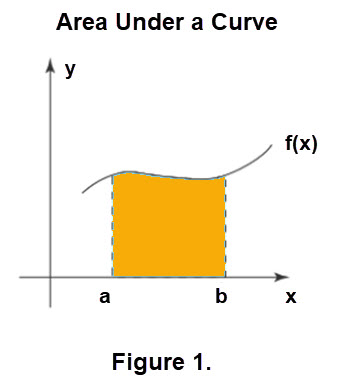
We will briefly discuss a simple situation. Suppose we have a graph of a function displayed on a grid, but without an algebraic expression for the graph. Let's represent the graph by the name \(y = f(x)\) as in Figure 1 shown below. Here we want to Approximate the Area between Curve \(y = f(x)\) and the x-axis over the interval \([a, b]\). (For this discussion we will use an \(f(x)\) that is above the x-axis.)

If we had an algebraic expression for our curve then using calculus we would compute the integral \(\int_a^b f(x) dx\). Instead we will approximate the area using a technique called Simpson's \(\mathbf{\frac{1}{3}}\) Rule which is a numerical method that approximates the value of a definite integral by using geometric quadratic polynomials. This method is named after the English mathematician Thomas Simpson (1710 - 1761). Simpson's Rule is based on the fact that given three points, we can find a quadratiic polynomial (a parabola) through those points. The result is that \[ \mathbf{ \int_a^b f(x) dx \approx \frac{b - a}{6} \Big[ f(a) + 4f\Big(\frac{a + b}{2}\Big) + f(b)\Big]. }\]

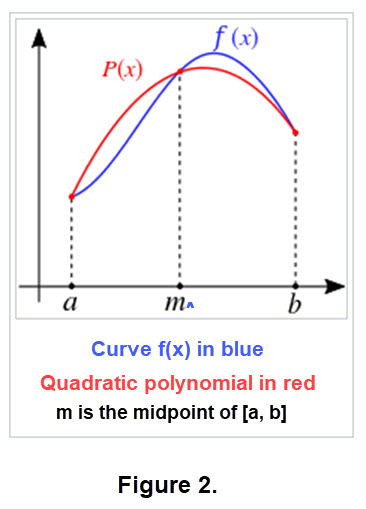
In Figure 2 we illustrate that if we can estimate the y-coordinates of the three distinct ordered pairs \((a, f(a))\) , \((\frac{a + b}{2}, f(\frac{a + b}{2}))\), \((b, f(b))\) we can obtain the area over [a, b] between the graph of the (red) quadratic polynomial and the x-axis as an estimate of the area between the (blue) curve and the x-axis. It is known that for three distinct ordered pairs we can always compute the quadratic polynomial. (Figure 2 is a modified version of a figure in Wikipedia Simpson's Rule.)

We needed a formula for the quadratic to show the red curve, but we only need the estimated y-values of the three ordered pairs to get a numerical value for Simpson's \(\frac{1}{3}\) Rule.

For an example of Simpson's \(\frac{1}{3}\) Rule click the MP4 file

We showed the step-by-step process. We computed the parabola and then compared the areas under the curves. We chose the original curve using a formula which is not the case in most applications of Simpson's \(\frac{1}{3}\) Rule. To obtain the formula of parabola when you have three distinct points look at Parabola equations using 3 points.

An Optional Extension: If the interval of integration [ a , b ] in \(\int_a^b f(x) dx\) is in some sense "small", then Simpson's \(\frac{1}{3}\) Rule with n = 2 subintervals will provide an adequate approximation to the exact integral. By "small" we mean that the function being integrated is relatively smooth over the interval [ a , b ]. For such a function, a smooth quadratic interpolant like the one used in Simpson's rule will give good results.

However, it is often the case that the function we are trying to integrate is not smooth over the interval. Typically, this means that either the function is highly oscillatory or lacks derivatives at certain points (like sharp points). In these cases, Simpson's rule may give very poor results. (As in other similar situations we divide to conquer.) A way of handling this problem is by breaking up the interval [ a , b ] into n > 2 small subintervals. Simpson's rule is then applied to each subinterval, with the results being added together to produce an approximation for the integral over the entire interval [a, b]. This approach is called the composite Simpson's 1/3 rule. (Portions of these paragraphs are based on material in Wikipedia Simpson's Rule.)

To get a feel of the work needed for the composite Simpson's 1/3 Rule click this thumbnail .

Estimating the Volume of Solids and Simpson's 1/3 Rule: A geometric figure or shape that has a three-dimensional structure is known as a geometric solid. They occupy space. In simple words, they have volume. There is a wide variety of solids. A group of common solids that appear in mathematics at various levels can be seen by clicking the thumbnail .

A solid of revolution is a three-dimensional solid figure obtained by rotating a two-dimensional curve or shape around a fixed axis. This process is often used to find the volume of a solid by integrating the area of the curve or shape with respect to the axis of rotation. The curve or shape is typically rotated around a vertical or horizontal axis, and the resulting solid is called a solid of revolution. The axis of rotation can be any line, not just vertical or horizontal. The solid of revolution can be thought of as a stack of thin discs or cylinders, each with a cross-sectional area equal to the area of the curve or shape at a given point. The volume of a solid of revolution can be calculated using various methods, including the disk method and the shell method. The disk method involves summing the volumes of thin discs, while the shell method involves summing the volumes of thin cylindrical shells. (This paragraph was a AI-generated answer at Search via the Brave browser.

To see a very good animation of the disk method and the shell method click here for a peek followed by animations Volumes on mathdemos.org. (Two other techniques, the washer method and the cross section method are shown for other types of solids.}.

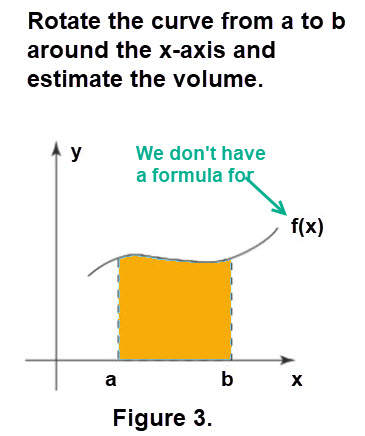
Lets focus on using the disk method using which rotates an area region about the x-axis. If we had a formula for the curve of the top of the area region then can use integration which is \[\mathbf{V = \int_a^b \pi (f(x)^2 dx}\]. Now lets imagine that we don't have a formula for function y = f(x) in Figure 3 below.

Using the integration formula shown above leads us to modify Simpson's 1/3 Rule to estimate the volume. All we need is to estimate three distinct ordered pairs \((a, f(a))\) , \((\frac{a + b}{2}, f(\frac{a + b}{2}))\), \((b, f(b))\). The modified rule is \[ \mathbf{V \approx \frac{\pi (b - a)}{6} \Big[ (f(a))^2 + 4(f\Big(\frac{a + b}{2}\Big))^2 +(f(b))^2\Big] }\]

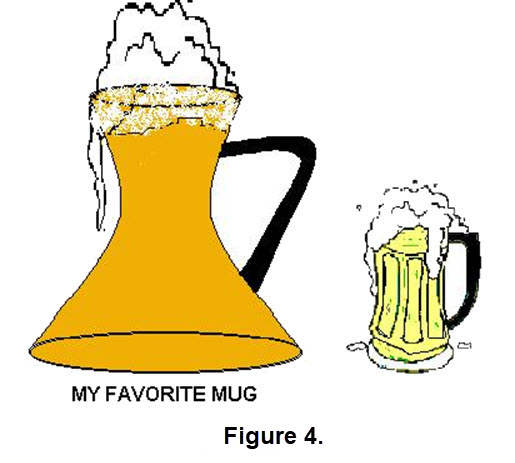
My Favorite Mug: Naturally we needed a mug that is appealing to our eyes and will quench our thirst so students can be enticed to read on. Thus the LARGE frosty beer mug was chosen for My Favorite Mug. The small is the STANDARD one.

We want to strip down, that is rearrange, our mug in such a way that we can approximate its volume of fluid using Simpson's 1/3 Rule.

Strip the mug image to set up a figure to use in the disk method.

• Rotate the mug image to be horizontal
• Strap off the foam
• Eliminate the handle
• Pretend we drain the 'beer'
• Pretend we put an x-axis down the center in 3D
• Erase portions to get a 1/2 2D image
• Label features for setting up Simpson's 1/3 Rule
• "Imagine" we perform the disk method to get the mug back!

To see the previous steps in action click the MP4 file

Finally, numerically use the data from the 12oz Standard mug to get the volume and the data from (your) My Favorite Mug to estimate the volume using Simpson's 1/3 Rule.

• Discuss the results with other class members.
• A Check: Fill MY FAVORITE MUG with water and measure the volume.
• Compare the measure with the approximation; discuss possible reasons for discrepancies.

Credits:

• This demo is a modification of a demo in the project Demos with Positive Impact , National Science Foundation's Course, Curriculum, and Laboratory Improvement Program under grant DUE 9952306. managed by David R. Hill and Lila Roberts. This demo was submitted by Dr. Klaus Volpert, Department of Mathematical Sciences Villanova University. The original demo appeared in 1999 and 2006.
• Extensions developed by David R. Hill.

Selected Resources

• Simpson's rule.
• More Simpson's rule.
• Integrals and Simpson's rule.
• Parabolic equations.
• Area under a curve.
• Nice discussion of the disk method.
• Nice discussion of shell method.
• Videos of the volume of solids.
• Solid geometry.
• Integral calculator.

========================================================

David Hill 5/1/2024
FAVORITEMUG
https://mathdemos.org/