NEW DEMO
Exponential and Logarithmic Function Gallery
Lets take a look at the background of the two basic transcendental functions in this gallery. A transcendental function is a mathematical function that cannot be expressed as a finite combination of algebraic operations, such as addition, subtraction, multiplication, division, raising to a power, and extracting a root. (An algebraic function is a function that involves only these operations.) Examples of transcendental functions include the exponential function, the natural logarithm, and the trigonometric functions. (There are others.) (A portion of this introduction appeared in Transcendental Function.) For a trig function gallery click here TRIG GALLERY.
Both of our "basic" functions have a long history and have changed their formulation as more mathematical topics provided added improvements. Changes occurred from varied sources like Egypt, Islamic Golden Age, Persian mathematicians, Archimedes, Greece, India, and through out the 15th-18th centuries. As things evolved the basic functions became intertwined so that we have a pair of functions which play important roles in mathematics and a variety of fields like astronomy, physics, economics, biology, chemistry, physics, and computer science, with applications such as compound interest, population growth, chemical reaction kinetics, wave behavior, public-key cryptography, radioactive decay, measuring earthquakes, measuring sound decibels, and measuring pH balance. (A portion of this paragraph appeared in Some History.)
The exponential function is a mathematical function denoted by \( f(x) =exp(x)\) or \(e^x\) (where the argument \(x\) is written as an exponent). The functions \(f(x)=b^x\) for positive real numbers \(b\) are also known as exponential functions. The natural base \(e = exp(1) =2.71828…\) is a ubiquitous (Being or seeming to be everywhere at the same time.) mathematical constant called Euler's number. To distinguish it, \(exp(x)= e^x\) is called the exponential function or the natural exponential function. The constant was discovered by the Swiss mathematician Jacob Bernoulli while studying compound interest. The exponential function is one of the most important functions in mathematics but the linear function ranks even higher in importance. (Portions for this paragraph came from Exp Function, Exponentiation, more Exp Function, and Math Constant.)
The history of logarithms is the story of a correspondence between multiplication on the positive real numbers and addition
on the real number line that was formalized in seventeenth century Europe and was widely used to simplify calculation
until the advent of the digital computer.
The Scottish mathematician John Napier published his discovery of logarithms in 1614.
His purpose was to assist in the multiplication of quantities that were then called sines.
E. W. Hobson called it "one of the very greatest scientific discoveries that the world has seen".
Henry Briggs introduced common or natural (base 10) logarithms, which were easier to use than the original Napierian logarithms.
Tables of logarithms were published in many forms over four centuries.
The idea of logarithms was also used to construct the slide rule, which became ubiquitous in science and engineering until the 1970s.
Optional Comments:
If you haven't seen a slide rule or couldn't find your slide rule, click here
.
(This is my 1960 slide rule with case. It was a bit dusty.I needed it for Calculus I.)
For directions on using a slide rule click here
How to use a slide rule.
The first hand held calculator was invented in 1967. But it weighed 55 pounds and cost $2,500. It needed more work.
For a bit of history click here
Early calculator.
"Resonable" hand held calculators were available in 1972-73. The Texas Instrument's SR-10 cost me $100.00.
I got it to use with the first Numerical Analysis course that I taught. Of course the students did not have one.
Click here
for a picture. (I dusted this off also.)
The natural logarithm with base \(e \cong 2.71828\) and written \(ln\)), however, continues to be one of the most useful functions in mathematics, with applications to mathematical models throughout the physical and biological sciences. A breakthrough generating the natural logarithm required the assimilation of a new function into standard mathematics. (Portions of these paragraphs came from History of logarithms and Britannica logarithm.)
Previously, we said our basic transcendental functions were intertwined. The function \(\mathbf{y = log_{a}(x)}\) is the inverse of the function \(\mathbf{y = a^{x} }\). In other words,
|
"whenever these make sense". That is, we have restrictions regarding domains and ranges of our basic functions.
|
For more information click here Further details.
The gallery contains two particular equations based on the exponential function.
The logistic equation or logistic curve is a common S-shaped curve.
The logistic equation (sometimes called the Verhulst model or logistic growth curve) is a model of population growth
first published by Pierre Verhulst (1845, 1847).
The logistic equation appears in a wide range of fields like ecology, chemistry, demography, economics,
geoscience, probability, sociology, political science, linguistics, and statistics.
For more information click here
Logistic equation.
The second equation is called the normal density function.
"A normal distribution is sometimes informally called a bell curve."
"The term "standard normal", which denotes the normal distribution with zero mean and unit variance came into general use around the 1950s,
appearing in the popular textbooks by P. G. Hoel (1947) Introduction to Mathematical Statistics and A. M. Mood (1950) Introduction to the Theory of Statistics.
Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known."
For more information click here Normal distribution.
Exponential and Logarithmic Gallery
The following is a gallery
of demos for illustrating selected families of functions. These figures and animations can be used by instructors in a classroom setting or by
students to aid in acquiring a visualization background relating to the change
of parameters in expressions for functions. Two file formats, gif and MP4, are used and should run on most systems. Originally, see the NOTES below the
gallery of animations, the animations were gif files which had no control for a user. The animations are now MP4 files which allow the user to easily control features
like stop and go, restart, and change the animation screen size. The controls are similar to those in You Tube. Click this thumbnail
to see an example.
Gallery of Animations
| \(\text{General exponential function}\) \( \mathbf{ \color{red}{h(x)=a^x}}\) \( \mathbf{ \color{green}{f(x)=a^x+b}}\) |
|
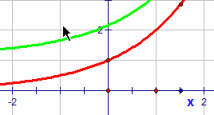
Vary a
MP4 Animation Vary b MP4 Animation |
| \(\text{Exponential function base e}\) \( \mathbf{ \color{red}{h(x)=a*e^{x+b}}}\) \( \mathbf{ \color{green}{f(x)=a*e^{x+b}}+c}\) |
|
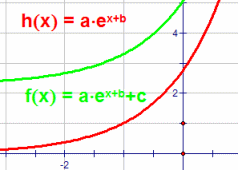
Vary a
MP4 Animation Vary b MP4 Animation Vary c MP4 Animation |
| \(\text{Natural logarithm function}\) \( \mathbf{ \color{red}{h(x)=a*ln{(x+b)}}}\) \( \mathbf{ \color{green}{f(x)=a*ln{(x+b)}}+c}\) |
|
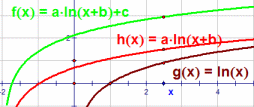
Vary a
MP4 Animation Vary b MP4 Animation Vary c MP4 Animation |
| \(\text{Negative exponential family}\) \( \mathbf{ \color{green}{r(x)=}\color{red}{a}\color{green}{*}\color{green}{(1-e^{-\color{red}{b}\color{green}{*x})}}}\) |
|
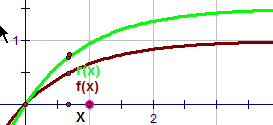
Vary a
MP4 Animation Vary b MP4 Animation |
| \(\text{Logistic equation family}\) \(\mathbf{ \color{green}{r(x) = } \frac{\color{red}{C} } { \color{green}{1 +} \color{red}{A} \color{green}{* e^{- bx} } } }\) |
|
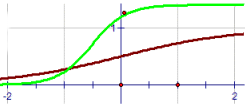
Vary A
MP4 Animation Vary b MP4 Animation Vary C MP4 Animation |
| \(\text{Normal density function}\) \(\mathbf{ \color{green}{r(x) = e^{\frac{-(x-\color{red}{A} \color{green}{ )^2} }{b} } } }\) |
|
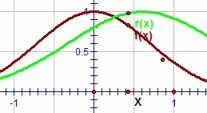
Vary A
MP4 Animation Vary b MP4 Animation |
NOTES
- This demo is a modification of a demo in the project Demos with Positive Impact , National Science Foundation's Course, Curriculum, and Laboratory Improvement Program under grant DUE 9952306. managed by David R. Hill and Lila Roberts. The project was based on submitted ideas from instructors. The original demo appeared in 2006.
- Special thanks to Deane Arganbright of University of Tennessee at Martin and to Walter Hunter at Montgomery County Community College for their assistance with the development of the Excel files that were used to get this gallery. The book "Mathematical Modeling with Excel", by Erich Neuwrith and Deane Arganbright (Brooks-Cole) provides a rich source of information for developing Excel routines for mathematical instruction.
- This gallery was developed by David R. Hill, Temple University.
Selected Resources
- Transcendental Function
- Some History
- Exp Function
- Exponentiation
- more Exp Function
- Math Constant
- How to use a slide rule
- Early calculator
- History of logarithms
- Britannica logarithm
- Further details
- Logistic equation
- Normal distribution
- Where does e come from?
- Exp Function
- Exp Function again
- History Computer
- Slide Rule