NEW DEMO

The Secret to Solving Word Problems. Hint: It's Not about Math.

Solving word problems is far more about effective reading skills and far less about math. You might be asking, then, why do so many strong readers fear solving word problems? Because, math word problems have a perception problem.

Why Students Fear Solving Word Problems
Solving word problems doesn't feel like it "follows a rule" the way it does when you solve an equation. That can feel overwhelming to students who lack confidence in math. They just don't know how to get started. The good news for your readers is that there are rules they can follow (keep reading). Better still, the thinking they need to do is quite similar to the close reading that is required of them in English class. The key is to help them see it that way. In addition, a student's math fear can be very physical and not just in the "stomach ache" sort of way. When we are nervous, our short-term memory can freeze up. Realistically, solving word problems usually requires students to juggle more information in short-term memory than solving an equation: reading multiple lines of text, identifying what is being asked, picking numbers to use, and setting up an equation. All before they even begin to "do math". In short, that brain freeze might make them forget what they read, transcribe the wrong number, or write the wrong operation. They start to believe that they can't do math, when what they really need is help with short-term memory.

First, Fix the Perception Problem.
Share this secret with your students: Learn one set of rules for solving word problems in elementary school. And then you can use that same set of rules in every math class going forward. All you need are good reading skills to get you started. It's so important for your students to understand the difference between having difficulty with math and being nervous. Once they understand why "brain freeze" happens and that it has nothing to do with their math ability, they are less likely to view themselves as "bad at math". And then give them the one strategy that will always help: WRITE DOWN EVERYTHING YOU CAN. Simple as that. The more you put on the paper, the less you need to keep in short-term memory, and the less likely you are to forget a step or make a mistake.

Reliable Rules for Solving Math Word Problems
Now that you and your students have a clear sense of why they might struggle with solving word problems, here's a reliable set of rules they can follow to solve any problem.
1. Mark up the question. Circle the numbers you will use. Lightly cross out information you don't need. Underline exactly what you are asked to find. (e.g. If the question asks which student is tallest, your answer should be a name, not a number.) Use the same annotating skills you use in English class.
2. Draw a picture. You don't need to be an artist. For many students, there's truth to the saying "a picture is worth a thousand words". Pictures help most students visualize the problem. It clarifies what they are given and what they need to find. This strategy is particularly good for students with strong visual memory.

This introduction is from How to plan to help students for Word Problems.

This demo provides a toolbox of visual aids for geometrically oriented word problems. These visual tools are designed to help students develop equations that provide an algebraic model for the problem.

Level: Algebra, Precalculus, or Calculus courses in high school or college.

Prerequisites: Students should be familiar with fundamental relationships between components of geometric figures like triangles, rectangles, circles, rectangular solids, cylinders, cones, and spheres. The properties of similar triangles are also needed.

Instructor's or Student's Notes: We restrict our demos to measurement of geometric word problems.

Many students have difficulty developing an algebraic equation from the description provided in a word problem. Some of the difficulty stems from a lack of the geometric visualization skills required for the written description to be translated into a figure. An animation of the geometric construction process helps students focus on salient features involved, providing an opportunity to algebraically develop an equation describing the physical situation. With this in mind we have constructed a set of animations that illustrate standard geometric constructions that commonly occur in textbook word problems.

Many word problems that employ the use of geometric figures make use of common shapes like circles, triangles, rectangles, rectangular boxes, cylinders, and cones. Such word problems frequently involve perimeter, area, surface area, and/or volume. Many texts suggest that these concepts be reviewed to remind students of their meaning and to reacquaint students with appropriate formulas for computation. (Often a table of appropriate formulas is included, possibly in an appendix.) In addition, units of measurement should be reviewed. Understanding units of measurement assist students in developing appropriate equations from verbal descriptions in which units appear.

The skill of translating from verbal descriptions to algebraic equations is a prerequisite for success with optimization and related rate problems in calculus. Hence this demo can be used at various places in calculus courses prior to sections involving optimization and related rates. In some cases it may be appropriate to include practice formulating equations from verbal descriptions in early sections that deal with functions and graphs.

We start with a general outline of steps that apply to many verbal problems. (The steps listed below are really inter-related and are ordered merely as a guide so students have a starting point for aspects of the solution process.) The steps involved are illustrated with several examples. We then provide a collection of statements of geometrically oriented word problems together with visual demos that can be used within a lecture or assigned for students to use for practice. We expect the user to supply the algebra to accompany the situation. The animations can also be used as 'preview' material for optimization problems.

Outline of steps in a measurement geometric word problem.

1. Recognition: Each word problem has a "character" of its own. The diversity of situations to be modeled is an issue that tends to inhibit students from seeing a pattern for the solution process. Since we are dealing with a word problem the algebraic aspects are imbedded within verbal descriptions that connect various components of the problem. Students need some guide posts to assist with recognition. Several suggested guide posts that can useful are:

• Determine the geometric figure involved. Is it a plane figure or a solid?
• Is more than one shape or figure involved?

Certainly the recognition process depends on "reading the problem", which is often given as Step 1 in text books.

2. Read the problem: The reading of course must be accompanied by understanding. For beginning students one reading is rarely sufficient. The first reading can be used to get familiar with the general situation (the "character") of the problem.

• What type of measurement is involved? Perimeter, area, surface area, or volume?

A second (or later) reading can be used to focus on a formula that will be needed to perform the measurement involved. Here is where an accompanying animation as part of a lecture can provide practice with the visualization of measurement components. It is at this point that we usually tell the student to draw a diagram that is a geometric embodiment of the situation described in the problem statement. This is a key interpretive step and we need to devise ways for students to practice this step. (See some animations below.)

3. Label the diagram: Here the components of the diagram are to be identified as described in the verbal description. It important that the student correctly interpret which parts of the figure are known and which should be labeled with an unknown. In this step, using an animation as part of an example can aid in distinguishing between these two aspects of the problem.

4. Find an equation linking the quantities: The result of this step is completely dependent on the "character" of the problem. It is possible that two or more equations must be combined to get a single equation in a single variable that relates the quantities involving measurements. This is where the basic knowledge of perimeter, area, surface area, and/or volume formulas must be used. Ultimately we want one equation in a single unknown that models the measurement requested in the word problem.

Example 1. A large cylindrical can is to be designed from a rectangular piece of aluminum that is 25 inches long and 10 inches high by rolling the metal horizontally. (Hint:) Determine the circumference of the cylinder, the radius of the cylinder, the height of the cylinder, and the volume of the cylinder.

Many text books include a figure that indicates the rolling process as shown below.

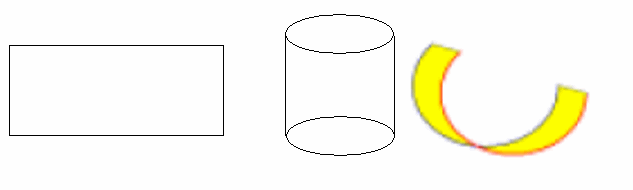
A simple animation of the process, click this thumbnail, gives a nice visual component that helps students determine relationships between parts of the rectangle and aspects of the solid. Incorporated as a demo within a lecture, the animation enhances the discussion of the necessary geometric relationships and facilitates development of the appropriate measurements. Rolling a sheet of paper is also a very effective prop in this case. For a detailed example of the 'rolling process' (record the data and try to get the answers to the questions) when you click the thumbnail video (View this mp4 file, there are some controls at the bottom).

Next, consider a general situation in which we know the volume of a cylinder to construct and need the area of the aluminum rectangular to bend. (This is an algebraic problem.)

A large can is to be designed to have volume

The lateral side of the can is formed by rolling a rectangle of

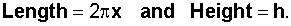
Word Problem: Find the values of x and h for which the smallest amount of material is needed. Now estimate --> the size of another piece of metal for the area of the top and bottom of the can.

In order to set up the equations for a general optimization problem we can draw upon the experience of the measurement word problem and its accompanying thumbnail animation. Having laid a foundation by the measurements in the word problem, the equations for the optimization problem are more readily constructed.

Example 2. A square sheet of material is to be used to construct a box with no top by cutting a square from each corner. Word Problem: If the material is 16 inches on a side, and a 3 inch square is cut from each corner, what is the volume of the box?

Many text books include a figure that indicates the process and the "finished box" as shown in the figure below.

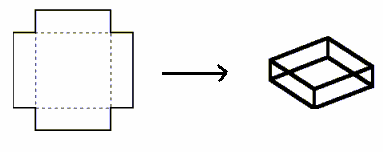
A simple animation of the process gives a nice visual component that helps students determine relationships between the original square of material, the corner cut-outs, and the finished box. Incorporated as a demo within a lecture the animation enhances the discussion of the necessary relationships and facilitates development of the appropriate measurements. It is easy to generalize the specific case to where a square of x inches is cut from each corner. Click the thumbnail video (View this mp4 file, there are some controls at the bottom).

A related exercise that appears in optimization problems is often phrased as follows.

Construct an equation for the following: A square sheet of material is to be used to construct a box with no top by cutting a square from each corner. If the sheet of the material is S units on a side and x is the size of the of an edge of the square corner, determine the value of x so that the box has maximum volume. (Here we focus on determining the equation; since this is an optimization problem and we need to use Calculus applied to the equation. To see the steps involving the use of derivatives click here Optimization Example)

The following is a gallery of demos for visualizing common geometric word problems that involve a measurement. These animations can be used by instructors in a classroom setting or by students to aid in acquiring a visualization background relating to constructing algebraic equations that model a word problem. The file format is mp4 so there are controls at the bottom of the animations. It is recommended that a viewer use the stop/start feature when incorporating the animations in a lecture format or when students view the animations on an individual basis.

\(\large{\text{General Problem Description}}\)	\(\large{\text{Animation Sample}}\)	\(\large{\text{Click mp4 File}}\)
\(\large{\text{Cylinder formed by }}\) \(\large{\text{rolling a rectangle}}\)		mp4 Animation
\(\large{\text{Box formed by}}\) \(\large{\text{cutting out corners}}\)		mp4 Animation
\(\large{\text{Cone formed by}}\) \(\large{\text{cutting out a sector}}\) \(\large{\text{of a circle}}\)		mp4 Animation
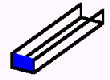
\(\large{\text{A gutter built by}}\) \(\large{\text{folding a rectangle}}\)		mp4 Animation
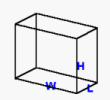
\(\large{\text{Surface area of a box}}\)		mp4 Animation
\(\large{\text{Cross-sectional area of }}\) \(\large{\text{an artery; fixed change}}\)		mp4 Animation
\(\large{\text{Cross-sectional area of }}\) \(\large{\text{an artery; percent change}}\)		mp4 Animation
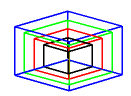
\(\large{\text{Cubic crystal growth}}\)		mp4 Animation

Credits:

• This demo is a modification of a demo in the project Demos with Positive Impact , National Science Foundation's Course, Curriculum, and Laboratory Improvement Program under grant DUE 9952306. managed by David R. Hill and Lila Roberts. The original demo appeared in 2002.
• Extensions developed by David R. Hill.

==================================================================

David R. Hill: click below to see more in mathdemos.org.

• Demos for instructors and/or students