An Optional Example:

Charles Monroe "Sparky" Schulz was an American cartoonist and creator of the comic strip Peanuts (which featured the characters Charlie Brown and Snoopy, among many others). He is widely regarded as one of the most influential cartoonists in History, and cited by many cartoonists as a major influence. "Peanuts pretty much defines the modern comic strip," states Bill Waterson "so even now it's hard to see it with fresh eyes. The clean, minimalist drawings, the sarcastic humor, the unflinching emotional honesty, the inner thoughts of a household pet, the serious treatment of children, the wild fantasies, the merchandising on an enormous scale – in countless ways, Schulz blazed the wide trail that most every cartoonist since has tried to follow." (Extracted from wikipedia; for more information click Wikipedia for Snoopy's author.

Often there are pictures of snoopy siting, but for our example we need snoopy lying down. See Figure 1. The profile of snoopy is the blue path atop the lying figure.

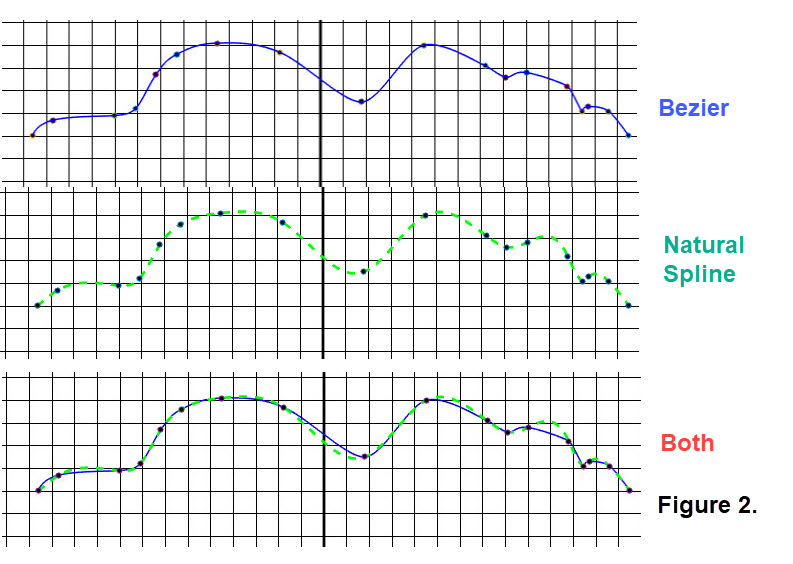
Consider the profile path in Figure 1 a function which we want to approximate using an interpolation curve. We first need to create a dataset, a set of ordered pairs along the profile. We carefully selected 18 ordered pairs where the profile is changing radiply. Figure 2 shows the interpolation using cubic Bézier, the interpolation using cubic natural splines, and a combination of the two interpolations. (We chose to use a smaller dot than those used previously to provide a closer look at the interpolations.)

Next we want introduce another interpolation scheme that use splines. The following is a modication of the description used for natural cubic splines.

General Description of Clamped Cubic Splines
A clamped cubic spline is a piecewise cubic function that is twice continuously differentiable. We require a dataset which satisfies the same three restrictions as those for natural cubic splines. The x-coordinates have the form \(x_0 < x_1 < x_2 < \dots < x_{n-1} < x_n\). Like natural splines we want to construct a cubic piecewise function S(x) where it is made up of the cubic pieces \(s_j(x)\) on the subintervals \( [x_j, x_{j+1}]\) for \(j \,= \,0, 1, 2, \dots , n-1\). This means that S(x) has the following form

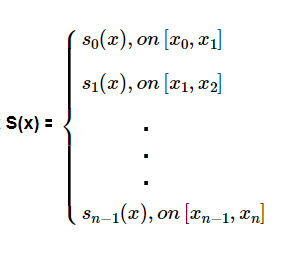
where \[s_j(x) = d_j(x-x_j)^3 + c_j(x - x_j)^2 + b_j (x - x_j) + a_j \; for \; j \,= \,0, 1, 2, \dots , n-1.\]

We require that:

• \(\textbf{S(x)}\) interpolates all the n + 1 points in the dataset.
• \(\textbf{S(x)}\) is continous on the interval \([x_0, x_n]\).
• \(\mathbf{S'(x)}\) is continous on the interval \([x_0, x_n]\).
• \(\mathbf{S''(x)}\) is continous on the interval \([x_0, x_n]\).
• \(\mathbf{S'(x_0)}\) = an assigned slope at \(x_0\) and \(\mathbf{S'(x_n)}\)= an assigned slope at \({x_n}\).

The requirements listed above guarantee that S(x) will generate a smooth curve.

Note in the last requirement at the first and the last x-coordinate we must supply a slope. This reqirement introduces more information into the interpolation scheme. In fact, you might say that you have a "control" at these points. This is similar to what we discussed in cubic Bézier interpolation.

Let's add another feature. We previously mentioned "divide to conquer". Looking at the profile of snoopy there appear to be two sharp points. So we can subdivide the profile into three regions. To use clamped cubic splines we need to assign slopes at each start and last point for each subdivision. Hence three clamped splnes are needed. Figure 3 shows this situation. (The figure is taken from Numeriical Analysis, 8th edition, by Richard L. Burden and J. Douglas Faires published by THOMSON * Brooks/Cole.)

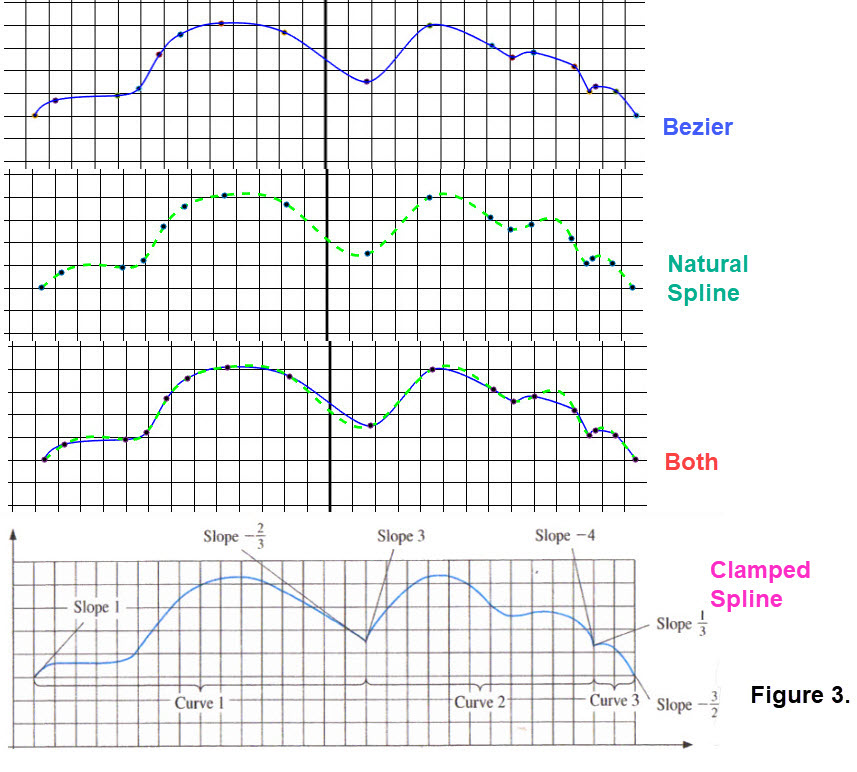
Inspect Figure 3, especially at spots where the clamped spline had assigned a slope. Subdividing into three curves helps at places where the profile has quick changes. At the intersection of curves 1 and 2 both the Bézier and the natural spline approximations make "round" changes. At the interection of curves 2 and 3 both the Bézier and the natural spline approximations appear to make a quick turn. For the region that is near the end of curve 2 the Bézier approximation is flatter than the natural spline approximation. Over all, the three interpolations a quite similar, but the clamped spline is best.

An intresting project would be to construct a grid based image of the profile of another figure. A chalenging figure like a camel standing or a cheetah running may be a good choice.